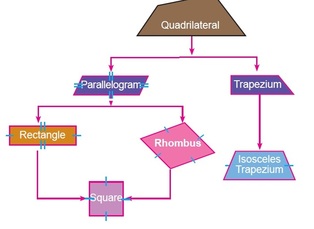
CBSE 8th Polygons+Quadrilateral+Parallelogram+Three Dimensional figures
Three-Dimensional Figures - Worksheets Download File
8th parallelogram worksheet and Assignments Download File |
| ||||||||||||||||
Practice: Polygons+Quadrilateral+Parallelogram+Three Dimensional figures
1. How many diagonals does each of the following have?
(a) A convex quadrilateral (b) A regular hexagon (c) A triangle
Answer: (a) 2 (b) 9 (c) 0
2. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? Using the formula: (n - 2)180°
3.What can you say about the angle sum of a convex polygon with number of sides?(a) 7 (b) 8 (c) 10
4. What is a regular polygon? State the name of a regular polygon of (i) 3 sides (ii) 4 sides (iii) 6 sides
5. Find the measure of each exterior angle of a regular polygon of (i) 9 sides (ii) 15 sides
8. How many sides does a regular polygon have if the measure of an exterior angle is 24°? Number of sides of a polygon =360/exterior angle
9. How many sides does a regular polygon have if each of its interior angles is 165°?
Exterior Angle = 180°-interior angle
10. (a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
(b) Can it be an interior angle of a regular polygon? Why?
[ If interior angle is 22° then the exterior angle = 180°-22°=158°On dividing 360° by 158° we can’t get answer in whole number, so such a polygon is not possible.]
(a) A convex quadrilateral (b) A regular hexagon (c) A triangle
Answer: (a) 2 (b) 9 (c) 0
2. What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? Using the formula: (n - 2)180°
3.What can you say about the angle sum of a convex polygon with number of sides?(a) 7 (b) 8 (c) 10
4. What is a regular polygon? State the name of a regular polygon of (i) 3 sides (ii) 4 sides (iii) 6 sides
5. Find the measure of each exterior angle of a regular polygon of (i) 9 sides (ii) 15 sides
8. How many sides does a regular polygon have if the measure of an exterior angle is 24°? Number of sides of a polygon =360/exterior angle
9. How many sides does a regular polygon have if each of its interior angles is 165°?
Exterior Angle = 180°-interior angle
10. (a) Is it possible to have a regular polygon with measure of each exterior angle as 22°?
(b) Can it be an interior angle of a regular polygon? Why?
[ If interior angle is 22° then the exterior angle = 180°-22°=158°On dividing 360° by 158° we can’t get answer in whole number, so such a polygon is not possible.]
11. (a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
[Answer: The polygon with minimum number of sides is a triangle, and each angle of an equilateral triangle measures 60°, so 60° is the minimum value of the possible interior angle for a regular polygon. For an equilateral triangle the exterior angle is 180°-60°=120° and this is the maximum possible value of an exterior angle for a regular polygon.]
12. Can a quadrilateral ABCD be a parallelogram if
(i) <D + <B=180? (ii) AB=DC= 8cm, AD= 4cm,and BC = 4.4 cm (iii) <A = 70 and <C = 65?
Answer:
(i)It can be , but not always as you need to look for other criteria as well.
(ii) In a parallelogram opposite sides are always equal, here AD BC, so its not a parallelogram.
(iii) Here opposite angles are not equal, so it is not a parallelogram.
13. The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
14. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
15. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
16. . The following figures GUNS and RUNS are parallelograms. Find x and y. (x=6 , y =9 )
17. In the given figure both RISK and CLUE are parallelograms. Find the value of x.{x=10}
18. State whether True or False.
a) All rectangles are squares
Answer: All squares are rectangles but all rectangles can’t be squares, so this statement is false.
(b) All kites are rhombuses.
Answer: All rhombuses are kites but all kites can’t be rhombus
(c) All rhombuses are parallelograms
Answer: True
(d) All rhombuses are kites.
Answer: True
(e) All squares are rhombuses and also rectangles
Answer: True; squares fulfill all criteria of being a rectangle because all angles are right angle and opposite sides are equal. Similarly, they fulfill all criteria of a rhombus, as all sides are equal and their diagonals bisect each other.
(f) All parallelograms are trapeziums.
Answer: False;
All trapeziums are parallelograms, but all parallelograms can’t be trapezoid.
(g) All squares are not parallelograms.
Answer: False; all squares are parallelograms
(h) All squares are trapeziums.
Answer: True
20. Identify all the quadrilaterals that have.
(a) four sides of equal length (b) four right angles
Answer:
(a) If all four sides are equal then it can be either a square or a rhombus.
(b) All four right angles make it either a rectangle or a square.
(b) What is the maximum exterior angle possible for a regular polygon?
[Answer: The polygon with minimum number of sides is a triangle, and each angle of an equilateral triangle measures 60°, so 60° is the minimum value of the possible interior angle for a regular polygon. For an equilateral triangle the exterior angle is 180°-60°=120° and this is the maximum possible value of an exterior angle for a regular polygon.]
12. Can a quadrilateral ABCD be a parallelogram if
(i) <D + <B=180? (ii) AB=DC= 8cm, AD= 4cm,and BC = 4.4 cm (iii) <A = 70 and <C = 65?
Answer:
(i)It can be , but not always as you need to look for other criteria as well.
(ii) In a parallelogram opposite sides are always equal, here AD BC, so its not a parallelogram.
(iii) Here opposite angles are not equal, so it is not a parallelogram.
13. The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
14. Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.
15. The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
16. . The following figures GUNS and RUNS are parallelograms. Find x and y. (x=6 , y =9 )
17. In the given figure both RISK and CLUE are parallelograms. Find the value of x.{x=10}
18. State whether True or False.
a) All rectangles are squares
Answer: All squares are rectangles but all rectangles can’t be squares, so this statement is false.
(b) All kites are rhombuses.
Answer: All rhombuses are kites but all kites can’t be rhombus
(c) All rhombuses are parallelograms
Answer: True
(d) All rhombuses are kites.
Answer: True
(e) All squares are rhombuses and also rectangles
Answer: True; squares fulfill all criteria of being a rectangle because all angles are right angle and opposite sides are equal. Similarly, they fulfill all criteria of a rhombus, as all sides are equal and their diagonals bisect each other.
(f) All parallelograms are trapeziums.
Answer: False;
All trapeziums are parallelograms, but all parallelograms can’t be trapezoid.
(g) All squares are not parallelograms.
Answer: False; all squares are parallelograms
(h) All squares are trapeziums.
Answer: True
20. Identify all the quadrilaterals that have.
(a) four sides of equal length (b) four right angles
Answer:
(a) If all four sides are equal then it can be either a square or a rhombus.
(b) All four right angles make it either a rectangle or a square.
21. Explain how a square is.
(i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle
Answer: (i) Having four sides makes it a quadrilateral
(ii) Opposite sides are parallel so it is a parallelogram
(iii) Diagonals bisect each other so it is a rhombus
(iv) Opposite sides are equal and angles are right angles so it is a rectangle.
22.. Name the quadrilaterals whose diagonals.
(i) bisect each other (ii) are perpendicular bisectors of each other (iii) are equal
Answer: Rhombus; because, in a square or rectangle diagonals don’t intersect at right angles.
23. Explain why a rectangle is a convex quadrilateral.
Answer: Both diagonals lie in its interior, so it is a convex quadrilateral.
24. ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C.
Answer: If we extend BO to D, we get a rectangle ABCD. Now AC and BD are diagonals of the rectangle. In a rectangle diagonals are equal and bisect each other.
So, AC = BD , AO = OC ,BO = OD, And AO = OC = BO = OD So, it is clear that O is equidistant from A, B and C.
(i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle
Answer: (i) Having four sides makes it a quadrilateral
(ii) Opposite sides are parallel so it is a parallelogram
(iii) Diagonals bisect each other so it is a rhombus
(iv) Opposite sides are equal and angles are right angles so it is a rectangle.
22.. Name the quadrilaterals whose diagonals.
(i) bisect each other (ii) are perpendicular bisectors of each other (iii) are equal
Answer: Rhombus; because, in a square or rectangle diagonals don’t intersect at right angles.
23. Explain why a rectangle is a convex quadrilateral.
Answer: Both diagonals lie in its interior, so it is a convex quadrilateral.
24. ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C.
Answer: If we extend BO to D, we get a rectangle ABCD. Now AC and BD are diagonals of the rectangle. In a rectangle diagonals are equal and bisect each other.
So, AC = BD , AO = OC ,BO = OD, And AO = OC = BO = OD So, it is clear that O is equidistant from A, B and C.
HTML Comment Box is loading comments...