|
IX Physics Chapter: Work Power and Energy
|
|
| ||||||||||||||||||||||||||||||||
9th Work energy and power problems and solutions
Q. 1. Why do living beings and machines need energy?
Ans: To perform work
Q. 2. What is work? Derive expression for work done
Ans: If force act on a body and body shows displacement, we can say that work is done. Work has only magnitude and no direction so it is called a scalar quantity.
Let a constant force F displace a body through a distance, s in the direction of the force
Let W be the work done.
Work done = force × displacement => W = F s
if F = 1 N and s = 1 m then the work done by the force is said to be 1 N m. or 1 joule
Work done against the gravity = w = mgh
Work done to keep body in motion = w = ½ mv2
Q. 3. What are the two factors needs to describe work?
Ans: (i) Force (ii) Displacement
Q. 4. Define 1 Joule?
Ans: 1 J is the amount of work done on an object when a force of 1 N displaces it by 1 m along the line of action of the force.
Q. 5. When can we say that work is positive or negative?
Ans: Work done is negative when the force acts opposite to the direction of displacement.
Work done is positive when the force is in the direction of displacement.
Q. 6. Write the expression for work done when force is applied at an angle with the horizontal direction?
Ans: Work = FS cos q(theta)
Q. 7. Write the conditions when work done will be zero?
Ans: (i)if Force = 0 (ii) Displacement = 0 (iii) if q = 90 degree [ if F act right angle to the displacement
Q. 8. Is work done if body rotates in circular path?
OR, is it possible that a force acts on a body still the work done is zero? Explain with an example.
Ans: when object in circular path, force acting on a body is always towards the center of circular path. Since object does not displace towards the centre of circular path. So, no work is done.
Q.9. How much work is done to raise 5 kg body by 2 m?
Ans: work is done to raise object= Potential energy of object = mgh = 5 x 9,8 x 2 = 98 J
Q. 10. How much work is done by a force of 10 N to displace a body by 2 m?
Ans: W = FS = 10 x 2 = 20N
Q. 11. Work done y a body of mass 10 kg to lift it through certain height is 490 J . Calculate the height through which the body is lifted?
Ans: W = mgh => h =w/(mg)= 490J/(10x9.8) = 5m
Q. 12. A force of 10 N acting on at angle 60 degreee with the horizontal direction displaces body 2 m along the surface of floor. Calculate the work done?
Ans = W = FS cos q = 10 x 2 x cos 60 degreee = 20 x ½ = 10 J [q denotes angle]
Q. 13. Calculate the amount of work done in drawing a bucket of water weighing 15 kg from a well of depth 30m.
Answer: Given, mass m = 15 kg ; Acceleration due to gravity, g = 9.8 m/s2 ; Height h = 20 m
Here, work is done against gravity, ⇒ W =mgh = 15 × 9.8 × 30 = 4410 joules = 4.41KJ
Q. 14. Calculate the work done to attain a car of velocity 30m/s having mass 100kg?
Ans: w = ½ mv^2 = ½ x 100 x 30 x 30 = 45000j = 45 KJ
Q. 15. No work is done by a person moving on a road while carrying box on his head. Justify
Ans : Force applied on the box does not cause any displacement to the box. Hence no work is done.
Q.16. what is energy. Write the kinds of energy?
Ans: Energy is the capacity of a body to do the work. If work is done on the body, energy of the body increases. If work is done by the body, energy of the body reduces.
Kinds of energy: Mechanical energy, Chemical energy, heat energy, Electrical Energy, nuclear energy, sound energy , Light energy etc
Q. 17. How much work is done by a man who tries to push the wall of house?
Ans: Since there is no displacement in wall there is no work done W = F x 0 = 0J
Q. 18. What are the kinds of mechanical energy?
Ans: There are two types of mechanical energy
(a) Energy possessed by an object due to its motion is called kinetic energy. Example -Kinetic energy of a hammer is used to drive a nail into the wall. Bullet fired from a gun can penetrate into a target due to its kinetic energy.
(b) The energy possessed by a body by virtue of its position or due to state of strain, is called potential energy.
Example: The work done to lift a body above the ground level gives the potential energy of the body. Eg. Weight lifting.
Water stored in reservoir has large amount of potential energy due to which it can drive a water turbine when allowed to fall down. This is the principle of production of hydro electric energy.
Q. 19. Derive the expression for potential energy of a body above the ground level.
Ans: Consider an object of mass m. It is raised through a height “h” meter from the ground.By applying force F, The object gains energy to do the work done (w) on it.
Work done = force x displacement
W = F x h (Since F= ma , a = g => F = mg)
W = m g h
Q. 20. Derive the expression for potential energy of a body above the ground level.
Ans: Let a body (ball) of mass m is moving with an initial velocity v. If it is brought to rest by applying a retarding (opposing) force F, then it comes to rest by a displacement S.
Let, Ek = work done against the force used to stop it.
Ek = F x S ---- (i)
But retarding force F = ma -----> (ii)
Let initial velocity u = v, final velocity v = 0
From III equation of motion
v^2 = u^2 + 2aS
Applying, 0 = v^2 – 2aS (a is retardation)
2aS = v^2
Displacement, S = v^2/2a ----> (iii)
Substituting (ii) and (iii) in (i)
Ek = ma x v^2/2a
Ek = ½ mv^2
Q.21. what kind of energy posses by the following
(a) Flowing water (b) Water stored in dam (c) Wrist watch
Ans: (a) KE (b) PE (c) PE
Q.22. A horse and a calf running with same speed. Which one of the two has more kinetic energy?
Ans: Horse; due to greater mass
Q.23. A bus and a car having same kinetic energy, which one of the two is moving, fast?
Ans: Car as its mass is less than that of bus.
Q. 24. A ball is thrown vertically upward and its velocity keeps on changing. What happen to the KE when its velocity will be zero?
Ans: Since velocity is zero kinetic energy will be zero
Q. 25. Is potential energy a vector or a scalar quantity ?
Ans: Scalar Quantity
Q. 26. Give two examples where a body possesses both, kinetic energy as well as potential energy.
Ans: (i) flying areoplane has both K.E and P.E. (ii) A flying bird has both the energies
Q. 27. What do you mean by thermal Energy?
Ans: All matter contains particles, such as atoms or molecules. The particles in matter are always moving. As a result, these particles have energy that is due to their motion. The energy of the particles in matter due to their continual motion is thermal energy. The thermal energy in an object increases when the object’s temperature increases.
Q.28. When we cut a log of wood with a saw it becomes warm, why?
Ans: When we cut a log of wood with a saw mechanical energy converted into heat energy
Q. 29. Why do our hands become warm when rubbed against each other? Explain
Ans: When we run our hands it became warm as mechanical energy converted into heat energy
Q, 30. State and verify law of the conservation of energy?
Ans: LAW OF CONSERVATION OF ENERGY
Energy can neither be created nor destroyed, but it is transformed from one form to another. Alternatively, whenever energy gets transformed, the total energy remains unchanged.
Proof – Freely falling body
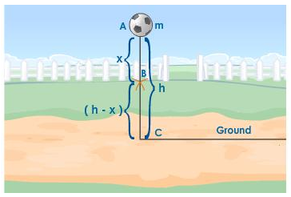
Consider a body of mass m falls from a point A, which is at a height h from the ground as shown in fig.
At A,
Kinetic energy Ek = 0 and Potential energy Ep = mgh
Total energy E = Ep + Ek = mgh + 0 = mgh
During the fall, the body is at a position B. The body has moved a distance x from A.
At B,
Velocity v^2 = u^2 + 2as
Applying, v^2 = 0 + 2ax = 2ax
Ek = 1/2 mv^2 =1/2 m x 2gx = mgx
Potential energy E p = mg (h – x)
Total energy E = Ep + Ek
= mg (h-x) + mgx
= mgh – mgx + mgx
E = mgh
If the body reaches the position C.
At C,
Potential energy E p = 0
Velocity of the body C is v^2 = u^2 + 2as
u = 0, a = g, s = h
Applying v2 = 0 + 2gh = 2gh
Kinetic energy Ek = 1/2 mv^2 = 1/2x m x 2gh Ek = mgh
Total energy at C
E = E p + E k
E = 0 + m g h
E = m g h
Thus sum of potential and kinetic energy of freely falling body at all points remains same.
Q.31. A man whose mass is 50 kg climbs up 30 steps of a stair in 30 s. If each step is 20 cm high, calculate the power used in climbing stairs
Ans: Mass of man=50 Kg ; g=10m/s^2
1 step = 20cm Þ 30 steps= 600 cm =6m => h=6m
w= mgh => w= 50 x 10 x 6
But , t=30 sec => p = w/t => p=50 x 10 x 6/30 => P =100 W
Q. A ball is dropped from a height of 10 m.if energy of the ball reduces by 40% after striking the ground , how high can the ball bounce back? {g = 10ms-2}
Ans: On reaching the ground the energy of the object = the energy at the top [law of conservation of energy]
Energy at the top = potential energy = mgh = m x 10 x 10 = (100m) joule [ let mass be m]
Loss of energy = 40% of (100m) Joule
Energy left = 60% of 100 x = 60/100 x 100m = 60m
Now the energy of the object on reaching the top again will be equal to that at the surface = 60m
but height will differ
Ep = mgh = m x10 x h So, 60 m = m x 10 x h => 60m / 10 x = h => h = 6 meter
:. The ball bounces back to 6m.
Q. A man drops a stone of mass 2 kg from the top of a building of height 15m when it reaches the ground, find its kinetic energy. How?
Solution: u = 0 m/s
v^2 = u^2 + 2as => v^2 = 2 x 10 x 15 = 300
KE = ½ mv^2 = 0 .5 x 2 x 300 = 300j
S= ut +1/2 at^2
15 = 0×t + 1/2 ×10 ×t^2
15= 5t^2
3 = t^2
√3= t
1.73 sec =t
Q. Two balls have different masses but same kinetic energy. which has more momentum? Justify your answer
The relation between momentum (p), mass (m) and kinetic energy (E) for a body is given as
p = (2mE)^1/2
Thus, we have p ∝ E^1/2
and also p ∝ m1/2
so, momentum is directly proportional to the square root of mass.
Now, for body 1
p1 = (2m1E1)^1/2
And for body 2
p2 = (2m2E2)^1/2.
Thus, if two body have same kinetic energies (E1 = E2) the one with greater mass will have more momentum
Q. A ball fall from a height 10m , strike the ground and rise back to height 8m. Find out the loss of mechanical energy
PE at Top = mgh = m × 10× 10 = 100m Joule
PE at height 8m = m × 10 × 8 = 80 Joule
Loss of energy = 100m - 80m = 20j
% loss og energy = 20%
Q. 1. Why do living beings and machines need energy?
Ans: To perform work
Q. 2. What is work? Derive expression for work done
Ans: If force act on a body and body shows displacement, we can say that work is done. Work has only magnitude and no direction so it is called a scalar quantity.
Let a constant force F displace a body through a distance, s in the direction of the force
Let W be the work done.
Work done = force × displacement => W = F s
if F = 1 N and s = 1 m then the work done by the force is said to be 1 N m. or 1 joule
Work done against the gravity = w = mgh
Work done to keep body in motion = w = ½ mv2
Q. 3. What are the two factors needs to describe work?
Ans: (i) Force (ii) Displacement
Q. 4. Define 1 Joule?
Ans: 1 J is the amount of work done on an object when a force of 1 N displaces it by 1 m along the line of action of the force.
Q. 5. When can we say that work is positive or negative?
Ans: Work done is negative when the force acts opposite to the direction of displacement.
Work done is positive when the force is in the direction of displacement.
Q. 6. Write the expression for work done when force is applied at an angle with the horizontal direction?
Ans: Work = FS cos q(theta)
Q. 7. Write the conditions when work done will be zero?
Ans: (i)if Force = 0 (ii) Displacement = 0 (iii) if q = 90 degree [ if F act right angle to the displacement
Q. 8. Is work done if body rotates in circular path?
OR, is it possible that a force acts on a body still the work done is zero? Explain with an example.
Ans: when object in circular path, force acting on a body is always towards the center of circular path. Since object does not displace towards the centre of circular path. So, no work is done.
Q.9. How much work is done to raise 5 kg body by 2 m?
Ans: work is done to raise object= Potential energy of object = mgh = 5 x 9,8 x 2 = 98 J
Q. 10. How much work is done by a force of 10 N to displace a body by 2 m?
Ans: W = FS = 10 x 2 = 20N
Q. 11. Work done y a body of mass 10 kg to lift it through certain height is 490 J . Calculate the height through which the body is lifted?
Ans: W = mgh => h =w/(mg)= 490J/(10x9.8) = 5m
Q. 12. A force of 10 N acting on at angle 60 degreee with the horizontal direction displaces body 2 m along the surface of floor. Calculate the work done?
Ans = W = FS cos q = 10 x 2 x cos 60 degreee = 20 x ½ = 10 J [q denotes angle]
Q. 13. Calculate the amount of work done in drawing a bucket of water weighing 15 kg from a well of depth 30m.
Answer: Given, mass m = 15 kg ; Acceleration due to gravity, g = 9.8 m/s2 ; Height h = 20 m
Here, work is done against gravity, ⇒ W =mgh = 15 × 9.8 × 30 = 4410 joules = 4.41KJ
Q. 14. Calculate the work done to attain a car of velocity 30m/s having mass 100kg?
Ans: w = ½ mv^2 = ½ x 100 x 30 x 30 = 45000j = 45 KJ
Q. 15. No work is done by a person moving on a road while carrying box on his head. Justify
Ans : Force applied on the box does not cause any displacement to the box. Hence no work is done.
Q.16. what is energy. Write the kinds of energy?
Ans: Energy is the capacity of a body to do the work. If work is done on the body, energy of the body increases. If work is done by the body, energy of the body reduces.
Kinds of energy: Mechanical energy, Chemical energy, heat energy, Electrical Energy, nuclear energy, sound energy , Light energy etc
Q. 17. How much work is done by a man who tries to push the wall of house?
Ans: Since there is no displacement in wall there is no work done W = F x 0 = 0J
Q. 18. What are the kinds of mechanical energy?
Ans: There are two types of mechanical energy
(a) Energy possessed by an object due to its motion is called kinetic energy. Example -Kinetic energy of a hammer is used to drive a nail into the wall. Bullet fired from a gun can penetrate into a target due to its kinetic energy.
(b) The energy possessed by a body by virtue of its position or due to state of strain, is called potential energy.
Example: The work done to lift a body above the ground level gives the potential energy of the body. Eg. Weight lifting.
Water stored in reservoir has large amount of potential energy due to which it can drive a water turbine when allowed to fall down. This is the principle of production of hydro electric energy.
Q. 19. Derive the expression for potential energy of a body above the ground level.
Ans: Consider an object of mass m. It is raised through a height “h” meter from the ground.By applying force F, The object gains energy to do the work done (w) on it.
Work done = force x displacement
W = F x h (Since F= ma , a = g => F = mg)
W = m g h
Q. 20. Derive the expression for potential energy of a body above the ground level.
Ans: Let a body (ball) of mass m is moving with an initial velocity v. If it is brought to rest by applying a retarding (opposing) force F, then it comes to rest by a displacement S.
Let, Ek = work done against the force used to stop it.
Ek = F x S ---- (i)
But retarding force F = ma -----> (ii)
Let initial velocity u = v, final velocity v = 0
From III equation of motion
v^2 = u^2 + 2aS
Applying, 0 = v^2 – 2aS (a is retardation)
2aS = v^2
Displacement, S = v^2/2a ----> (iii)
Substituting (ii) and (iii) in (i)
Ek = ma x v^2/2a
Ek = ½ mv^2
Q.21. what kind of energy posses by the following
(a) Flowing water (b) Water stored in dam (c) Wrist watch
Ans: (a) KE (b) PE (c) PE
Q.22. A horse and a calf running with same speed. Which one of the two has more kinetic energy?
Ans: Horse; due to greater mass
Q.23. A bus and a car having same kinetic energy, which one of the two is moving, fast?
Ans: Car as its mass is less than that of bus.
Q. 24. A ball is thrown vertically upward and its velocity keeps on changing. What happen to the KE when its velocity will be zero?
Ans: Since velocity is zero kinetic energy will be zero
Q. 25. Is potential energy a vector or a scalar quantity ?
Ans: Scalar Quantity
Q. 26. Give two examples where a body possesses both, kinetic energy as well as potential energy.
Ans: (i) flying areoplane has both K.E and P.E. (ii) A flying bird has both the energies
Q. 27. What do you mean by thermal Energy?
Ans: All matter contains particles, such as atoms or molecules. The particles in matter are always moving. As a result, these particles have energy that is due to their motion. The energy of the particles in matter due to their continual motion is thermal energy. The thermal energy in an object increases when the object’s temperature increases.
Q.28. When we cut a log of wood with a saw it becomes warm, why?
Ans: When we cut a log of wood with a saw mechanical energy converted into heat energy
Q. 29. Why do our hands become warm when rubbed against each other? Explain
Ans: When we run our hands it became warm as mechanical energy converted into heat energy
Q, 30. State and verify law of the conservation of energy?
Ans: LAW OF CONSERVATION OF ENERGY
Energy can neither be created nor destroyed, but it is transformed from one form to another. Alternatively, whenever energy gets transformed, the total energy remains unchanged.
Proof – Freely falling body
Consider a body of mass m falls from a point A, which is at a height h from the ground as shown in fig.
At A,
Kinetic energy Ek = 0 and Potential energy Ep = mgh
Total energy E = Ep + Ek = mgh + 0 = mgh
During the fall, the body is at a position B. The body has moved a distance x from A.
At B,
Velocity v^2 = u^2 + 2as
Applying, v^2 = 0 + 2ax = 2ax
Ek = 1/2 mv^2 =1/2 m x 2gx = mgx
Potential energy E p = mg (h – x)
Total energy E = Ep + Ek
= mg (h-x) + mgx
= mgh – mgx + mgx
E = mgh
If the body reaches the position C.
At C,
Potential energy E p = 0
Velocity of the body C is v^2 = u^2 + 2as
u = 0, a = g, s = h
Applying v2 = 0 + 2gh = 2gh
Kinetic energy Ek = 1/2 mv^2 = 1/2x m x 2gh Ek = mgh
Total energy at C
E = E p + E k
E = 0 + m g h
E = m g h
Thus sum of potential and kinetic energy of freely falling body at all points remains same.
Q.31. A man whose mass is 50 kg climbs up 30 steps of a stair in 30 s. If each step is 20 cm high, calculate the power used in climbing stairs
Ans: Mass of man=50 Kg ; g=10m/s^2
1 step = 20cm Þ 30 steps= 600 cm =6m => h=6m
w= mgh => w= 50 x 10 x 6
But , t=30 sec => p = w/t => p=50 x 10 x 6/30 => P =100 W
Q. A ball is dropped from a height of 10 m.if energy of the ball reduces by 40% after striking the ground , how high can the ball bounce back? {g = 10ms-2}
Ans: On reaching the ground the energy of the object = the energy at the top [law of conservation of energy]
Energy at the top = potential energy = mgh = m x 10 x 10 = (100m) joule [ let mass be m]
Loss of energy = 40% of (100m) Joule
Energy left = 60% of 100 x = 60/100 x 100m = 60m
Now the energy of the object on reaching the top again will be equal to that at the surface = 60m
but height will differ
Ep = mgh = m x10 x h So, 60 m = m x 10 x h => 60m / 10 x = h => h = 6 meter
:. The ball bounces back to 6m.
Q. A man drops a stone of mass 2 kg from the top of a building of height 15m when it reaches the ground, find its kinetic energy. How?
Solution: u = 0 m/s
v^2 = u^2 + 2as => v^2 = 2 x 10 x 15 = 300
KE = ½ mv^2 = 0 .5 x 2 x 300 = 300j
S= ut +1/2 at^2
15 = 0×t + 1/2 ×10 ×t^2
15= 5t^2
3 = t^2
√3= t
1.73 sec =t
Q. Two balls have different masses but same kinetic energy. which has more momentum? Justify your answer
The relation between momentum (p), mass (m) and kinetic energy (E) for a body is given as
p = (2mE)^1/2
Thus, we have p ∝ E^1/2
and also p ∝ m1/2
so, momentum is directly proportional to the square root of mass.
Now, for body 1
p1 = (2m1E1)^1/2
And for body 2
p2 = (2m2E2)^1/2.
Thus, if two body have same kinetic energies (E1 = E2) the one with greater mass will have more momentum
Q. A ball fall from a height 10m , strike the ground and rise back to height 8m. Find out the loss of mechanical energy
PE at Top = mgh = m × 10× 10 = 100m Joule
PE at height 8m = m × 10 × 8 = 80 Joule
Loss of energy = 100m - 80m = 20j
% loss og energy = 20%
HTML Comment Box is loading comments...

