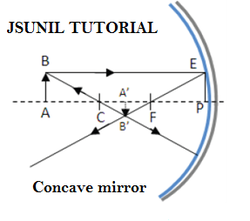
 Mirror formula is the relationship between object distance (u), image distance (v) and focal length. 1/v + 1/u = 1/f In Triangle ABC and Triangle A’B’C <A = <A’ = 900 <C =<C ( vert. opp. <s] Triangle ABC ~Triangle A’B’C [AA similarity] => AB /A’B’ = AC/A’C ----(I) Similarly, In Triangle ABC and A’B’C <A = <A’ = 900 <C =<C ( vert. opp. <s] Also, in Triangle ABC ~Triangle A’B’C [AA similarity] AB /A’B’ = AC/A’C ----(1) Similarly, In DFPE ~ A’B’F EP /A’B’ = PF/A’F AB /A’B’ = PF/A’F [ AB=EP] ----(II) From(i) &(ii) AC/A’C = PF/A’F => A’C/AC = A’F/PF => (CP-A’P)/(AP- CP) = (A’P – PF)/PF Now, PF = -f ; CP = 2PF = -2f ; AP = -u ; and A’P = -v Put these value in above relation: [(-2f) –(-v)] /(-u)-(-2f) = {(-v) –(-f) }/(-f) => uv = fv +uf => 1/f = 1/u + 1/v you may also see (a) Mirror formula (b) Mirror Formula
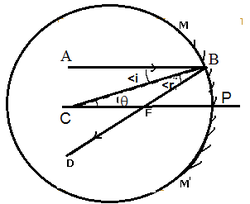 Derivation or Proof-of- the relation between focal length and radius of curvature(X) physics [R=2f] Consider a ray of light AB, parallel to the principal axis, incident on a spherical mirror at point B. The normal to the surface at point B is CB and CP = CB = R, is the radius of curvature. The ray AB, after reflection from mirror will pass through F (concave mirror) or will appear to diverge from F (convex mirror) From the figure, According to law of reflection,< i = <r <i = <q [Since, AB IICP] => <r= <q So, In D BCF, CF = BF ----(i) If the aperture of the mirror is small, B lies close to P, BF = PF (ii) From (i) and (ii) CF = FP Now, PC = PF + FC = 2 PF or R = 2f
35 Comments
a.waleeed
10/6/2014 04:06:08 pm
good proof
Reply
JSUNIL
14/10/2014 11:37:43 am
<A = <A’ = 90 degree
Reply
Himanshu
2/12/2016 05:40:38 pm
Not 900 it's 90 degree
Reply
pj
3/11/2014 11:08:07 am
Why is cf and bf are equal
Reply
aashray narang
12/2/2015 04:53:10 am
becoz they are the radii of same circle which passes through C B AND P
Reply
aashray
26/2/2015 12:33:30 pm
actually i =theta and i is =r implies theta equals to r and in triangle cfb theta is equal to r implies cf =bf because sides opp to eqaul angles are equal
Reply
ABHISHEK
6/11/2014 11:20:22 pm
Very nice and smart
Reply
aashray narang
12/2/2015 04:27:00 am
p is pole which lies on the mirror bt here it is not lying on the mirror. so do we neglect this small distance and is this is the reason that we consider a small aperture of much bigger radius of curvature
Reply
aashray
26/2/2015 11:32:00 am
i mean the second reason
Reply
navin
13/4/2015 11:38:58 am
How UV=fv+uf
Reply
Abhishek
1/10/2017 11:02:10 pm
Take common f then equation became uv/f=v+u , now divide the whole equation by uv, it gives mirror formula.
Reply
Adarsh Anand
15/4/2015 02:17:33 pm
i like your proof
Reply
sampath goud bommagani
21/5/2015 04:18:59 pm
Good explanation.can be understood very easily.....
Reply
Barghav
19/7/2015 08:11:29 am
Hdshhdirtyine
Reply
26/8/2015 10:21:17 am
when AB parallel to the principalaxis incident we can prove where we AB chose in down we can prove yes or no
Reply
jayant
27/12/2015 08:19:11 pm
why is bf=pf
Reply
Ram
29/9/2017 05:07:11 pm
It is because the distance of each part of the mirror from the focus are considered equal .
Reply
jatt
4/9/2016 10:10:09 pm
Derive mirror formula when object is on the focus
Reply
Tathya
10/10/2016 12:10:12 pm
If we have a applied sign conventions in the formula so why there is need to apply again in the formula ...
Reply
Rahul kumar
9/11/2016 04:47:55 pm
It's really absolute proof of mirror formula
Reply
suraj singh
21/11/2016 04:57:38 pm
this is very good method
Reply
rishav goenka
25/11/2016 07:59:47 pm
Why a=a'=900 ??
Reply
srishti
30/11/2016 03:31:30 pm
How can we say bf=pf
Reply
Ani
30/11/2016 06:36:55 pm
In the second one, how is BF=PF, I didn't understand that,
Reply
war
23/2/2017 08:27:55 pm
BF=PF because F is the common point to points B and P
Reply
bashir
8/5/2017 10:36:26 pm
Confusion...Is it that in BCF,bf+fc=BC. But how is this possible that in a triangle sum of 2 sides = the third one. It is only possible when the points r colinear.
Reply
mahima
28/7/2017 09:48:25 pm
I just want to know that is there any case that the second ray which passes through the centre of curvature reflects back to any other direction??
Reply
Abhijit kumar sharma
25/11/2017 11:55:41 pm
Very good froof
Reply
Amit Singh
14/5/2018 07:13:23 am
Proof value of parallogram DFPE and ABF
Reply
Leave a Reply. |
Blog SeaRCH Link
All
Join Us For Update |
||||||


